What are Flux Lines?

We love talking about magnets. When we do, we often use magnetic field pictures to show what's going on. There's a lot of information to be learned from these images, but let's take a moment and examine them more closely.

What are those black lines circling around the magnet? What do they mean? What are they telling us? Follow the path of a fluxline with us, journeying from pole to pole.

Vectors: Strength and Direction

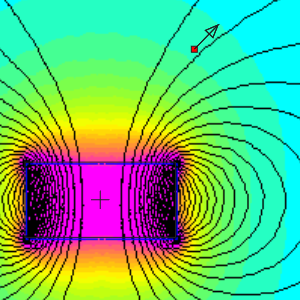
These pictures show us a lot of information for points all around a magnet. For a moment, let's just consider one point. If we measure the magnetic field at a single point, what are we measuring? The measured field is a vector - it has strength and direction.

How strong is the magnetic field? That's strength. It's typically expressed in gauss or tesla (1 tesla = 10,000 gauss). With no magnets around, a sensitive magnetometer measures the earth's magnetic field of around 0.5 gauss. Near a strong neodymium magnet, you could measure thousands of gauss.

In our magnetic field images, strength is shown with color.

The other half of the story concerns which way the magnetic field is pointing. Here on Earth's surface, we say the magnetic field is pointing north. Near a neodymium magnet that's much stronger, the magnet will dominate which way the compass points. Putting a magnet near your compass alters the reading.

Bonus points: You can recreate this image with our Magnetic Field Calculator by entering a diameter of 1", a thickness of 0.5", and x and y values of 0.625" and 1". It describes the field as acting at an angle, but also offers numbers breaking that angled vector into x and y components.

Why don't we use vectors?

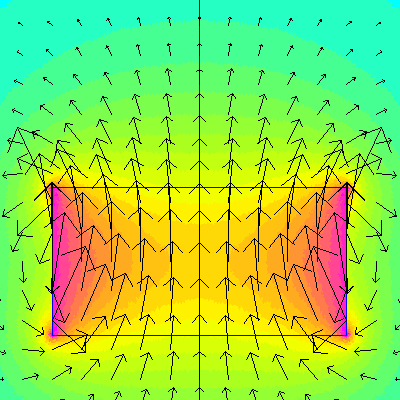
We can show the magnetic field direction by drawing arrows on the plot. Simply pick some grid of points, and use arrows to show the direction.

You can't show too many, or the arrows completely clutter things up. The number of arrows is more of an artistic choice, picking what shows the most information without too much clutter. Here we've drawn arrows on a regularly spaced grid.

Each arrow indicates the direction of the magnetic field at that point. The size of the arrow is proportional to the strength, so you really see two indicators of strength: arrow size and color.

How about those flux lines?

Flux lines are another way of depicting direction. Instead of a regularly spaced grid of arrows, we draw a path that follows the magnetic field direction, always progressing in the direction of the local field.

Imagine walking across the earth's surface with a compass in your hand, dragging a big piece of chalk to mark your path. Each step forward must be towards the north pole; follow the compass needle. You can imagine the paths we'd draw on the earth's surface. We would all start from wherever we're reading this, and all converge at the magnetic north pole somewhere up in the Arctic Ocean. See you there!

On a globe, you see how the lines converge on the pole. Locally, as lines drawn across a parking lot, they just look like parallel lines.

We can do the same exercise near a strong magnet. Imagine a tiny ant holding a compass, following the needle as it walks along. The result is a lot more interesting than our walk in the parking lot!

Near the magnet, the lines we draw will look like the familiar magnetic field diagrams, looping from one pole to the other. The lines that don't loop back around immediately head to Earth's poles, looping back around through the magnet only after walking the circumference of the earth!

When you finish, you know that at any point around the magnet, the compass needle should be parallel to the lines of flux.

We used a powerful 2" x 2" x 1" thick BY0Y0X0-N52 block magnet for this demonstration.

That's the story, but read on for a few more technical nuggets for the serious magnet nerds.

What's a Weber?

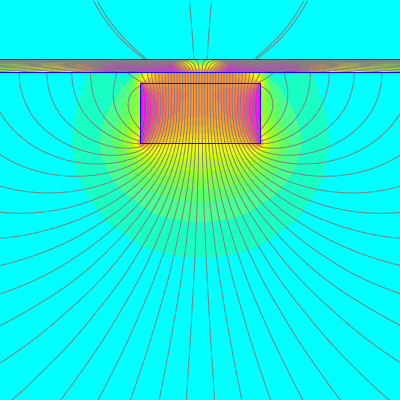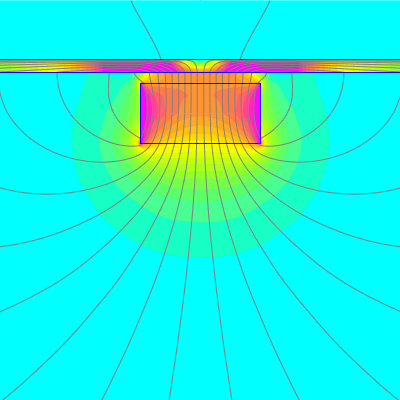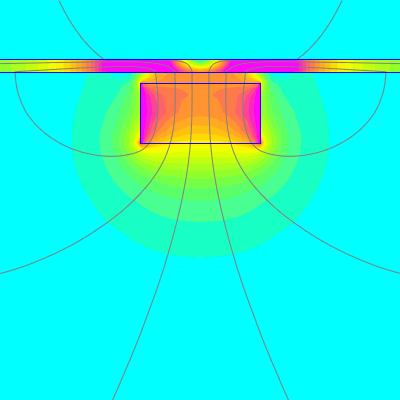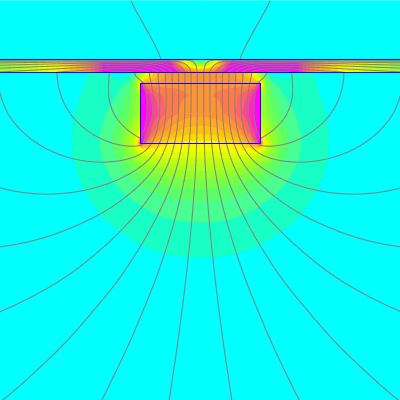
Back in the early history of studying magnets, the CGS system (pre-SI) described magnetic flux as some, "number of lines." It makes a certain kind of sense - the more flux lines you have going through some area, the more magnetic flux you have. This unit of measurement really isn't used anymore, but sometimes the nomenclature sticks around. We get asked, "How many lines of flux is in there?" These days, that's not really a thing.

You can say that the number of flux lines might be proportional to the magnetic flux, but not directly equal to. Pictures of the same magnetic field with 2 or 10 or 20 flux lines all are equally correct.

A Weber (wb) is a measure of how much magnetic flux is in an area. From our Unit Converter:

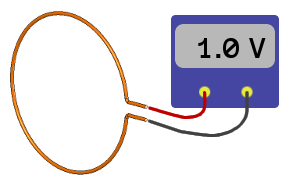
Imagine encircling an area with a circle of wire. If the magnetic flux in there changes by 1 weber in a second, you'll be able to measure 1 volt induced across the wire. So: 1 weber per second equals 1 volt in the circle of wire. Or: 1 Wb = 1 V s.

Note that nothing is mentioned about the size of the loop of wire. It doesn't matter if the loop of wire is one inch or one meter across. If you're measuring 1 volt across the wire, the magnetic flux is changing by 1 weber per second in there.

The gauss or tesla most of us are more familiar with is flux density, or weber per square meter. One tesla equals 1 weber per square meter. You might think of it as a density of lines entering an area, but really, try not to think of those lines as having a specific flux. Use them as indicators of direction.

Also keep in mind that even with all this talk about direction, and knowing that sometimes the math looks quite similar to that used for electrical circuits, there's nothing actually flowing here. The lines follow a path, but there's nothing physically flowing around, like water in a pipe or electric current in a wire.