Magnetic Table Legs
I'm building a table, and I want to attach the legs with magnets. What magnets should I get? How much pull force do I need?
These sounds like simple questions, but the answers get complicated quickly. They depend very much on the details of how you do it. Let's build a small footstool to see what's involved.
While customers aren't exactly banging our door down asking for magnetic footstools, this example illustrates a concept that comes up surprisingly often.
Let's build one quickly to get straight to the problem.



The top of this footstool has four steel discs inset on the underside. We used our NSWX02 steel washers, which are 1-1/8" in diameter.
Each of the four legs has a 1" diameter, RX033CS-N countersunk ring magnet set in the top. This combination sounds like a strong choice. In fact, trying to pull one of these magnetic legs straight away from the base requires 15-20 lb of pull force!
That impressive figure doesn't help avoid the main problem with this footstool: It is incredibly easy to tip over. Even if we chose magnets two or five times more powerful, it would still be too easy to collapse the stool by wiggling around on it.
This is not a safe footstool.
Let's build a better one.


Footstool #2 uses the same steel washers and the same magnets. The new feature is a kind of collar where a leg attaches. It's a 1-1/2" tall block with a hole in it, just barely big enough for the leg to slide in. This mechanical collar prevents the tipping motion.
If we repeat our pull force test, we see the same result as the first footstool. This makes sense, because the added block doesn't change the magnetic attraction force between the magnet and the steel washer. (We measured slightly higher because of a little binding of the leg in the hole, thanks to the snug fit.)
In resistance to tipping, however, this new design is far superior. How hard can we push the leg before it snaps off? This depends more on the material strength of the wood than the magnetic connection. It will tip when something breaks!
This second footstool is much safer. We wouldn't mind using it ourselves.
See both in action in this video!
Aren't we stating the obvious?
With a magnetic connection, it often makes sense to have some mechanical support in addition to the magnetic attraction. This example illustrates the vast difference in real world performance that's possible with different mechanical designs, using the exact same magnets.
It also illustrates how some magnet questions are not able to answered with a single pull force number. Both of those footstools use the same magnets with the same pull force, but with very different results.
People often think of using magnets for connecting things that will snap in place and come apart easily. Maybe they want to connect two tables together to make a larger table. Or try connecting two pieces of a sectional couch. Or a magnetic catch for an outdoor gate.
The problem with these ideas is that, without the right mechanical arrangement like our footstool, it can be hard to execute. The connection needs to be strong enough to resist coming apart during normal use, yet weak enough so that attaching them is easy, safe and fun. You can't have the magnetic attraction be an easy to pull apart, 5-10 lb strength, while simultaneously having a 50-100 lb strength required to hold pieces together during use.
The problem is obvious once you start trying it out, but the solutions are subtly mechanical, not magnetic.
The story can end here, but read on for...
Technical Notes: How to Calculate Tipping Forces
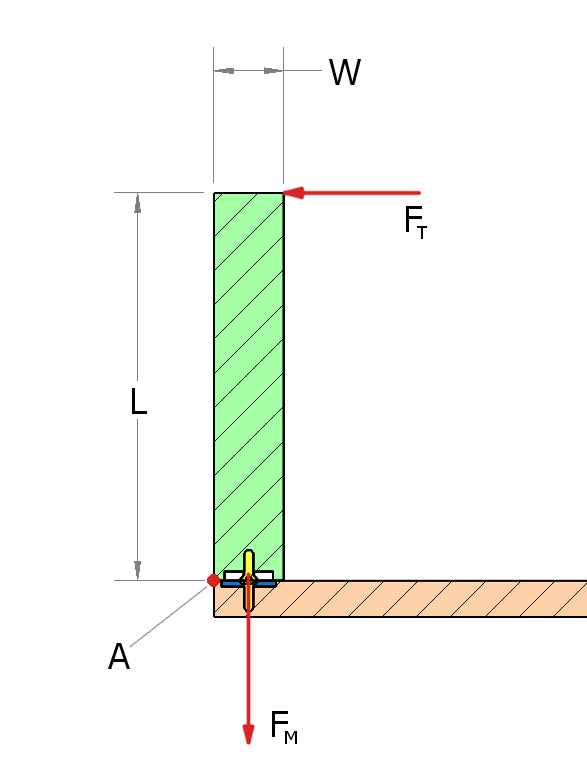
How would you calculate the force required to tip a table or footstool leg? Let's use methods learned in a mechanical engineering Statics course. Even if you haven't taken such a class, this way of thinking about leverage is something most folks understand intuitively, even without the math.
The diagram shows the forces involved with a single footstool leg. There's a green leg of length L with a width of W. The magnet pulls down with force FM. The force we push the leg with our finger is FT.
In the instant when the magnet first breaks free, we imagine this footstool leg rotating about point A. Sure, there's no actual hinge mechanism there, but it will tend to start rotating around that point when we push hard enough.
We simplify the problem by only considering torque about point A. Torque is a force multiplied by a distance. Torque = Force x Distance. That's why a longer wrench requires less push to turn a bolt.
At the instant just before the magnet breaks free, the torques are perfectly balanced. The torque of the magnet holding the leg in place is perfectly opposing the torque from pushing the top. Restated mathematically, the sum of these torques (or moments in the jargon of Statics) must equal zero at the balancing point.
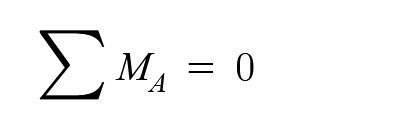
Let's write out the two torques. The force from pushing with our finger, FT, pushes at a distance (moment arm) of L, rotating about point A. Let's say counter-clockwise rotation is positive here, so the first part is FT x L.
Next, the force of the magnet is acting with a moment arm of half the width of the leg. We write this as negative, since this torque is acting in the clockwise direction.
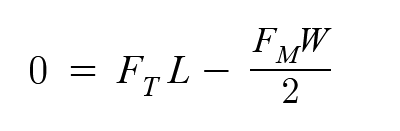
This straightforward formula contains mostly things we know. We know the size of the leg, L & W, and if we have picked a magnet (we used the RX033CS-N ring magnet), we can use its pull force as FM.
With a little algebraic manipulation, we solve for FT, the force required to tip the leg over.
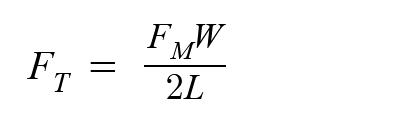
We can now estimate the force required to tip this a long leg over, knowing the dimensions of the leg and the magnet force.
Let's double-check ourselves, plug some numbers in and see how well they match our test. The listed Pull Force, Case 1 for the RX033CS-N magnet is used, though that is a little higher than what we actually get attracting to the steel disc. The disc has less steel than our big test plate.
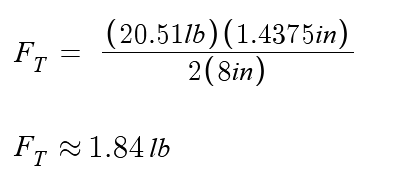
Our direct measurements were 1.1 - 1.2 lb, so we're definitely in the right ballpark!
