Magnetic Dipole Moment
What is the magnetic dipole moment of a magnet?
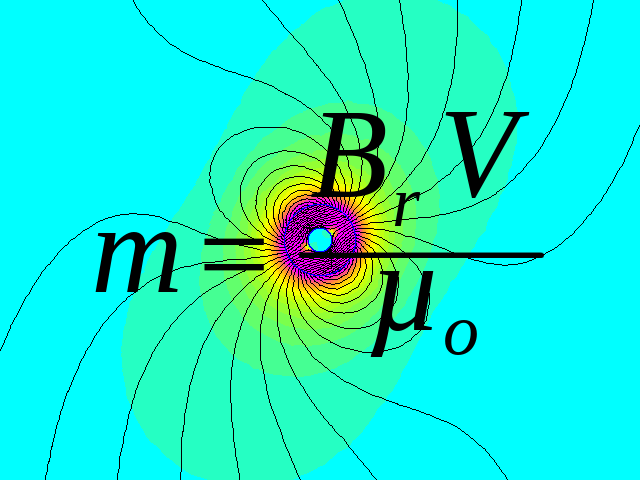
Let's be specific: What is the magnetic dipole moment of a 1/2" diameter x 1/8" thick D82 disc magnet? It's not listed on the D82 page, but we can calculate it using our Pull Force Calculator as 0.422 A m2. You can also calculate it using the formula, also mentioned in our glossary.
OK, but what does that mean?
The Wikipedia article defines a magnetic dipole as:
...the limit of a closed loop of electric current (or a pair of poles) as the size of the source is reduced to zero while keeping the magnetic moment constant.
Whew, that's a mouthful! While that definition might satisfy the mathemeticans among us, we're looking for a more practical, working definition. Let's try rephrasing our Calculator's answer to make some sense of it.
The magnetic dipole moment of a D82 magnet is 0.422 A m2.
We're not fond of the word dipole in this context, even though we use it ourselves. There might be less confusion on this topic if we just say it has a magnetic moment of 0.422 A m2, dropping the word "dipole" entirely. We'll come back to dipoles later.
The magnetic dipole moment of a
D82 magnet is 0.422 A m2.
Also, this word "moment" sounds like jargon. It's a fancy word that physicists and engineers use when they really mean "torque." It's a force applied at a distance, like foot-pounds of torque applied with a wrench.
The magnetic moment torque of a
D82 magnet is 0.422 A m2.
While we're at it, those units of amperes x meters squared sound strangely electrical for something that's supposed to be a torque. It's equivalent to newton meters per tesla (N m / T). That's torque per magnetic field strength.
The magnetic torque of a D82 magnet is 0.422 newton meters per tesla (N m / T).
With all due respect to the metric system, we could just as well express torque in inch pounds.
The magnetic torque of a D82 magnet is 3.74 inch pounds per tesla (in lb / T).
If you stick this magnet in some external magnetic field, it will tend to feel a (maximum) torque of about 3.74 inch pounds for every tesla of magnetic field strength.
See the moment torque in action!
With a D82 magnet sitting on my desk, the only external magnetic field is the earth's magnetic field, with a strength of about 0.5 gauss (0.00005 tesla). That means, in addition to the gravity pulling it the magnet down to the surface of my desk, the magnet also feels a torque that tries to twist it to align with Earth's magnetic field.
How strong is this torque?
0.422 N m / T * 0.00005 T = 0.00002 N m = 0.003 in oz
That's a really tiny torque. Even so, if you set a disc magnet on its edge on a wood desk, it will rotate to align with the magnetic field. It's a tiny force, but we can see it in action! This old video first appeared in our article, Which Pole is North?
If we place magnets into stronger magnetic fields, we'll observe stronger forces. Check out this video from our Circular Halbach Arrays article.
For another interesting demonstration, consider a diametrically magnetized magnet rolling on a flat surface. It doesn't roll smoothly. It seems to wobble, accelerating and slowing down periodically as it rolls. It mimics the way something might roll if it weren't perfectly round, though this magnet isn't oval shaped.
As it's rolling, the magnetic torque is trying to align the magnet to the ambient magnetic field, just like a compass needle points north.
What is a dipole moment?
We dropped that word "dipole" without much discussion earlier. We see "dipoles" mentioned in a lot of places. What exactly does it mean?
To answer it, let's drop the word "moment" and just ask, what is a magnetic dipole?
From our Glossary:
Some folks (like physicists) use a magnetic dipole model to simulate or mathematically model a magnet or group of magnets. Mathematically, it's easier than considering the complexities of weird magnet shapes. It's not theoretically perfect. Using it won't always match measured field strengths near a neodymium magnet. It works great for a sphere, but isn't correct near other shapes like discs or blocks. It's a great approximation when you're measuring far away from a magnet, but not so good close up, especially near the edges of a magnet.
In other words, a "dipole moment" is a mathematical model of a magnet. Working from first principles, smart folks derived some equations that describe the magnetic field around a magnet, or around 2 point charges, or around a coil of wire with current flowing through it (electromagnet) - the math works out the same for each.
Another word that's used is "equivalent." One might say a D82 magnet has an equivalent magnetic dipole moment of 0.422 A m2. It's a strength to plug into those dipole equations to get a result similar to what we'd expect with a D82 magnet.
Show me the math of this model!
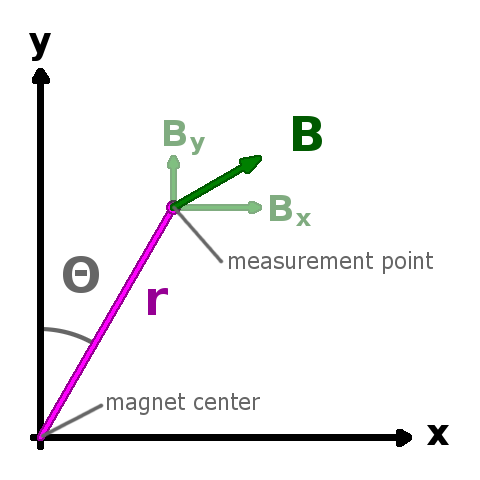
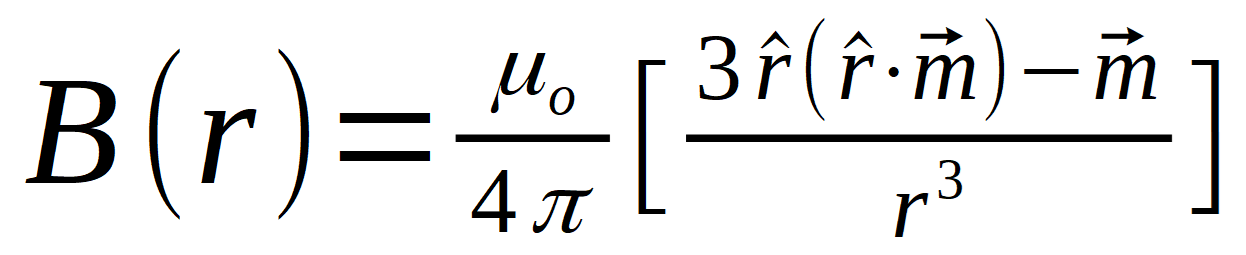
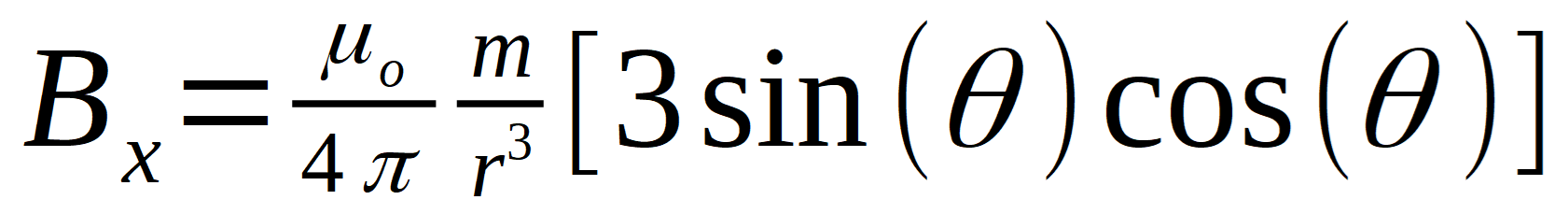
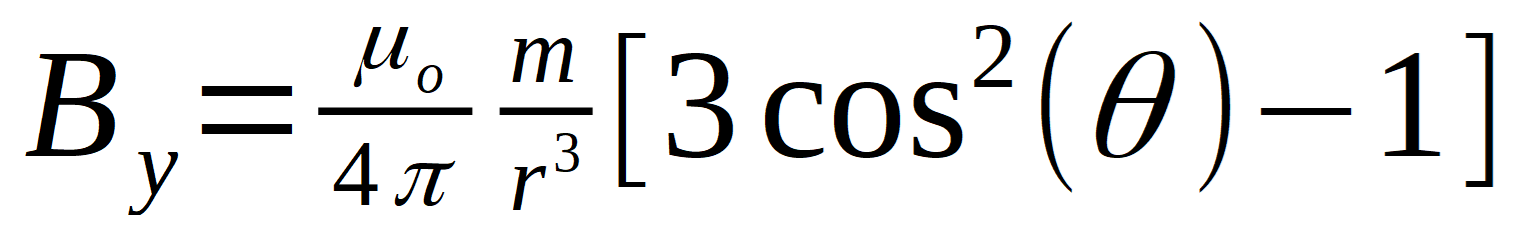
There's a good summary in the Wikipedia article on the subject. A concise formula is given there using vector terms. They've added some detail to the formula originally found in J.D. Jackson's Classical Electrodynamics, 1975.
Using this formula, we can calculate the field strength at any point in free space around this theoretical magnet, where the point's location is defined with a distance from the magnet's center, r, and an angle from the vertical magnetization direction, ?. Assume the magnetization direction is pointing straight up the Y axis.
For those of us who have forgotten vector math and dot products, let's write that out into two simpler terms. This breaks the vector field strength and direction into two values, the field strength in the x and y directions.
There is no magnetic field strength in the "Z" direction, out of the page/screen. Bz = 0.
- µo is the permeability of a vacuum, or 4 p x 10-7 N/A2.
- r is the distance from the magnet's center to the measurement point.
- m is the magnetic moment of the magnet we're considering.
How good is this dipole model?
It's very good, except when it isn't.
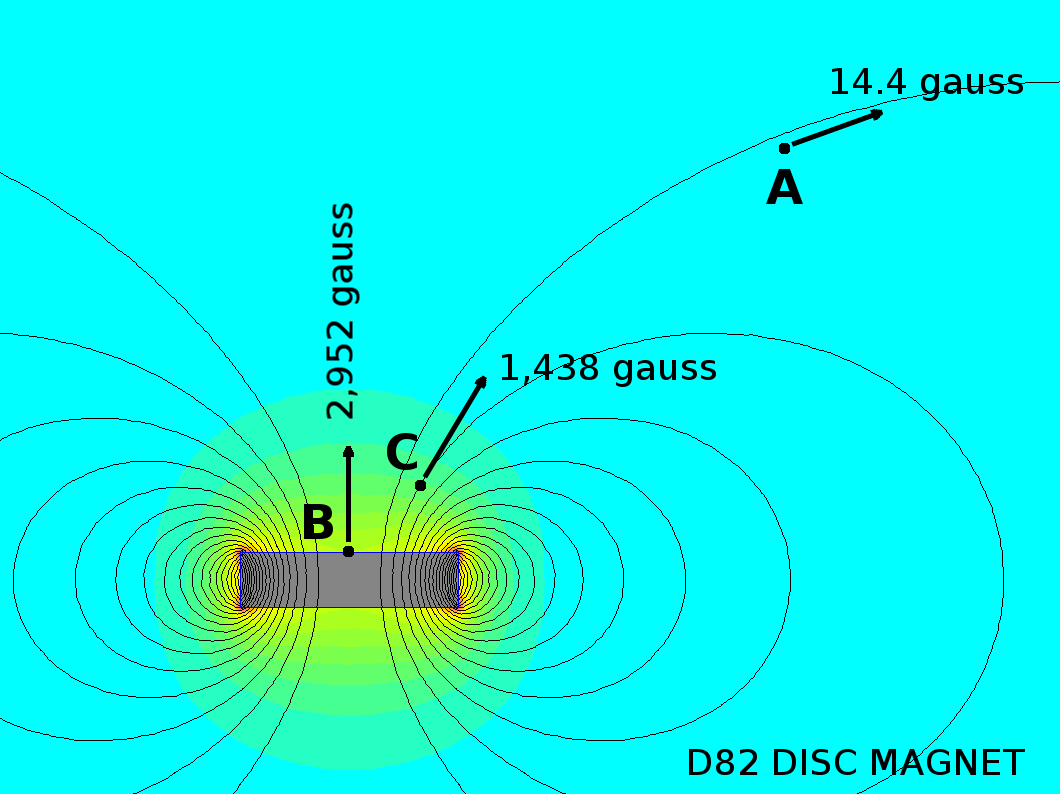
The first image shows the magnetic field strength and direction around a D82 disc magnet. It is a 2D slice through the center of the magnet. Field strength is shown with colors, while direction is always parallel to the black lines of flux (see What are Fluxlines).
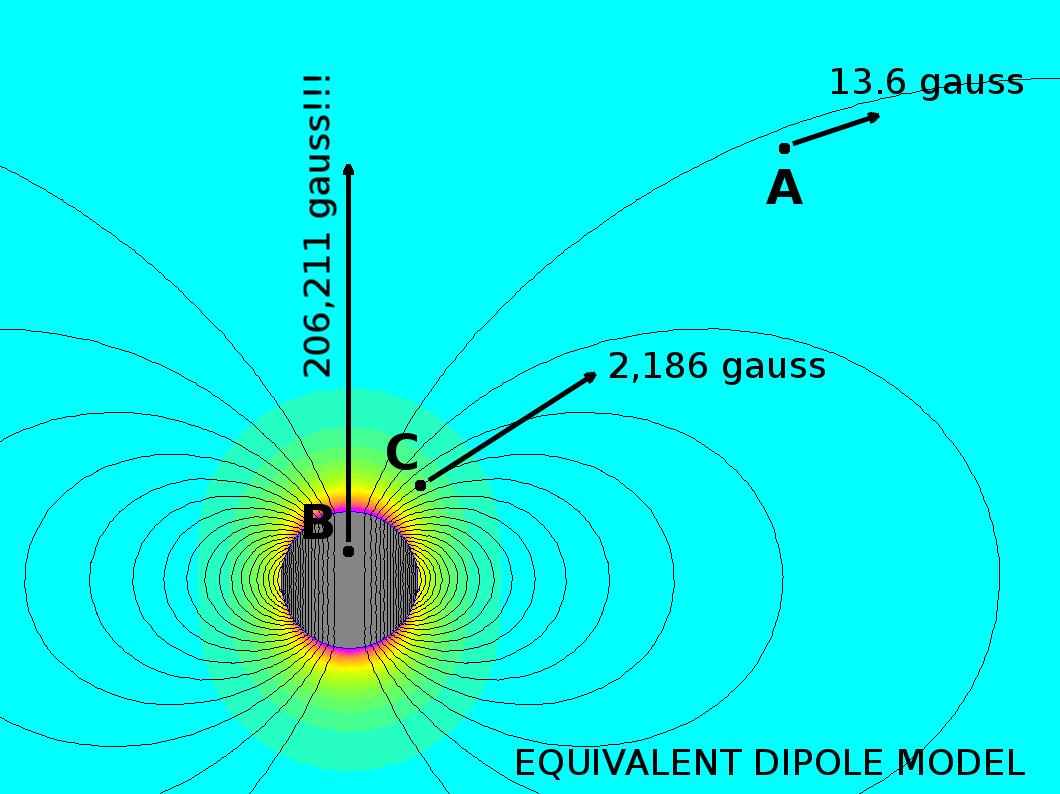
The dipole model allows us to calculate field strength and direction around an "equivalent dipole." That's shown in the second picture.
Without doing any math, we see that the dipole model looks just like a sphere magnet. That's true - the way the math works out under the hood, it's assuming the magnet is shaped like a sphere. Assume a spherical cow.
It's also visible that the model is a great approximation when measuring some distance away from the magnet, but not so accurate closer in.
- Point A is looks good, with a magnitude within 5%.
- The dipole model gives nonsensically high values for point B, as if it were inside some theoretical magnet. It's meaningless, and shouldn't be interpreted as an accurate representation of reality.
- The dipole model gives a reasonable sounding answer for point C, but it doesn't match the thin disc in either magnitude or direction. The more the magnet shape differs from a sphere, the more these calculations won't match reality.
Rule of Thumb: How close to the magnet can I use the dipole model?
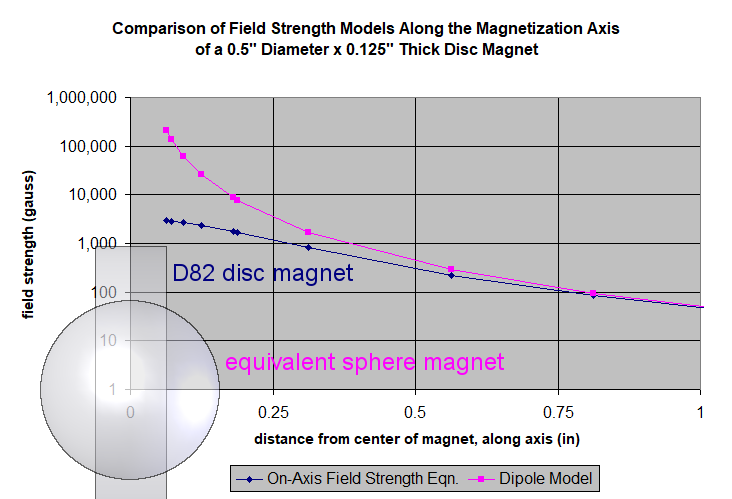
Comparing our simulation results with the dipole model, we can make up some rough guidelines. If you only need to get the magnitude within 5%, you're good for distances of 1" or more from the center of the magnet. If you need smaller errors more like 1%, be at least 3" away from the center of the magnet.
Your results may vary. The accuracy depends very much on the shape of the magnet. Our guess is to go out to at least 2x a magnet's largest dimension to be within 5%, and 6x the magnet's largest dimension to be within 1%.
Honorable mention:
Our Surface Fields article gives equations for the field strength along the magnetization axis of various magnet shapes. For off-axis values, our online Magnetic Field Calculator is a handy tool. Neither of these helpful guides use the dipole model. They depend on the magnet's shape!
Folks running their own simulations often ask us for either the magnetization (M) of a magnet, or the dipole moment (m). It's confusing how convention uses the same letter to denote two very different things.
- Magnetization, frequently denoted with a capital M, is like a material property of a magnet. It does not change with the magnet's size or shape. M = Br / µo, expressed in amperes per meter (A/m).
- Dipole moment, denoted with a lower case m, does depend on the volume of the specific magnet. M = Br V / µo, in ampere meters squared (A m2).
